本文讲解Ford-Fulkerson算法的思路
分析
朴素算法
朴素的想法
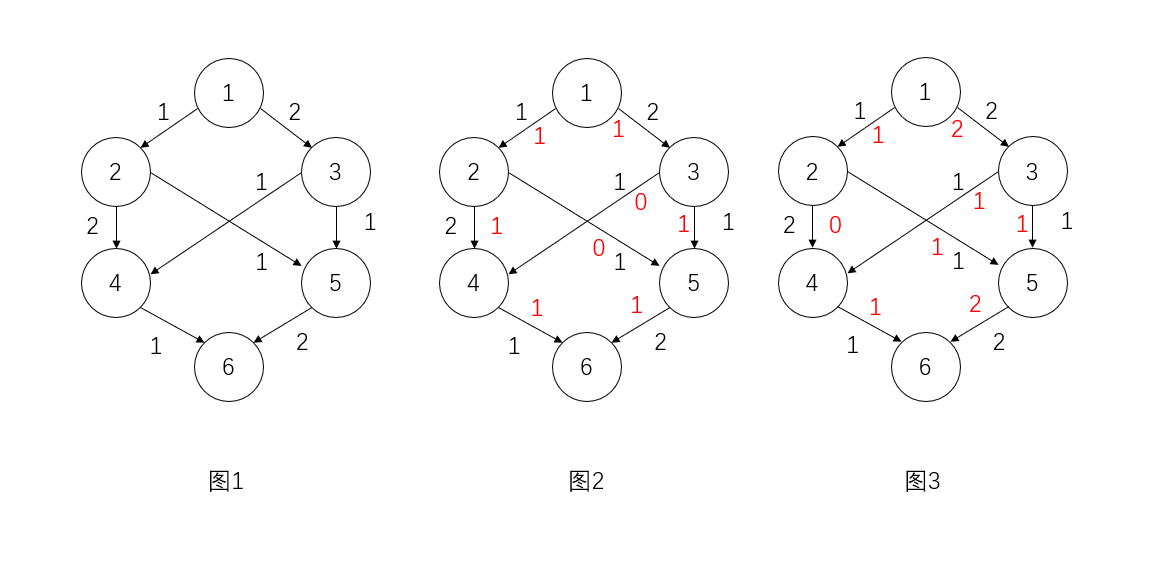
上面的图中
所以上述的算法是错误的
改进
观察图3
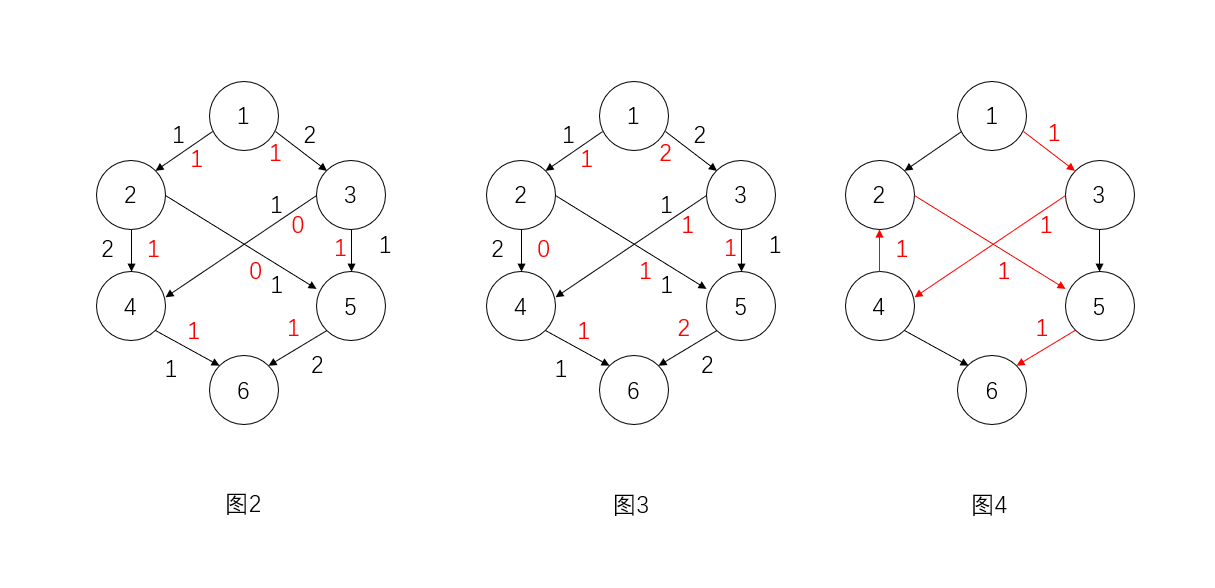
从图4看
解释
仔细观察图2和图3
所以
上面的做法
于是对一个流
算法描述
对网络上的每个流$G(V,E)$
Ford-Fulkerson算法
输入
网络$G$ : 一个图$G(V,E)$ ( $E$中的边$e$有权重$w_e\in\mathbb{N_+}$ , ) $max\_flow=0$ , 输出
该网络上的最大流的流量$f$ : 步骤0. [建立反向边]定义$max\_flow\gets0$
用邻接表G[V]存储网络 , 对$E$中的每条边$e=\langle u,v\rangle$ ; 作其反向边$e'=\langle v,u\rangle$ , 并置$w_{e'}\gets0$ , 。 步骤1. [寻找增广路]在$G$上DFS
寻找从$s$到$t$的简单路径 , 要求该路径上每条边可用权值$(w_e-f_e)$大于0 , 若找到 。 记该路径上的权值最小的边权值为$f$ , 否则$f\gets0$ , 。 步骤2. [找到了
更新残余网络]如果$f>0$ , 置$max\_flow\gets max\_flow+f$ , 对路径上的每条边$e$ 。 置$f_e\gets f_e+f$ , 记其反向边为$e'$ 。 置$w_{e'}\gets w_{e'}+f$ , 返回1 。 。 步骤3. [没有找到]如果$f=0$
输出$max\_flow$ , 算法结束 , 。
最大流不会超过从$s$出发的所有边的边权和
证明
在Ford-Fulkerson算法结束后的残余网络上没有$s\rightarrow t$路径
结论1
结论2
对于任意一个流
而对于残余网络
也可以用反证法
至此
模板
#include <iostream>
#include <cstdio>
#include <vector>
#include <queue>
#include <cstring>
#define V 5005 //V为顶点最大个数<span class="bd-box"><h-char class="bd bd-beg"><h-inner>,</h-inner></h-char></span>视数据范围而定
#define INF 0x7fffffffffffffff
using namespace std;
typedef long long ll;
struct edge {
ll to, w, rev;
};
vector<edge> G[V];
int s, t;//源点和汇点<span class="bd-box"><h-char class="bd bd-beg"><h-inner>,</h-inner></h-char></span>是全局变量
bool vis[V];
ll max_flow();
ll dfs(ll u, ll f);
void add_edge(ll from, ll to, ll w);
ll dfs(ll u, ll f) {
if(vis[u]) return 0;
vis[u] = true;
if(u == t) return f;
for(int i = 0; i < G[u].size(); i++) {
edge &e = G[u][i];//注意是引用<span class="bd-box"><h-char class="bd bd-beg"><h-inner>,</h-inner></h-char></span>需要直接修改原图
if(!vis[e.to] && e.w > 0) {
ll curf = dfs(e.to, (f > e.w) ? e.w : f);
//min函数有些编译器不给过
if(curf > 0) {
e.w -= curf;
//直接修改容量而非同时记录f和w<span class="bd-box"><h-char class="bd bd-beg"><h-inner>,</h-inner></h-char></span>只是为了方便
G[e.to][e.rev].w += curf;
return curf;
}
}
}
return 0;
}
ll max_flow() {
ll maxf = 0;
while(true) {
memset(vis, 0, sizeof(vis));
ll f = dfs(s, INF);
if(f == 0) break;
maxf += f;
}
return maxf;
}
void add_edge(ll from, ll to, ll w) {
G[from].push_back(edge(to, G[to].size(), w));
G[to].push_back(edge(from, G[from].size() - 1, 0));
}
如有发现模板的错误请联系我指正